
Humans have always sought to make life easier for ourselves – it’s almost what defines us as a species. Part of this is to alleviate ourselves from the mundane tasks of life, from making a pot-stand so it does not have to be held over a fire, to having an automatic out of office reply on your email. As systems became more complex during the industrial revolution there was increased interest in the automatic control of such systems, one of which being the automatic steering of ships.
The steering of a ship could be controlled by aiming for a location, such as a port, and setting your compass bearing to that port: keep following the bearing and you reach the port, right? One problem with steering large ships is that they can be subject to large wind forces that cause the ship to drift over time, if the steering mechanism only uses a directional bearing it will take a longer route to reach its destination that it could have done. Furthermore, they have a lot of inertia: it takes quite a bit of effort to get them to change direction or slow down.
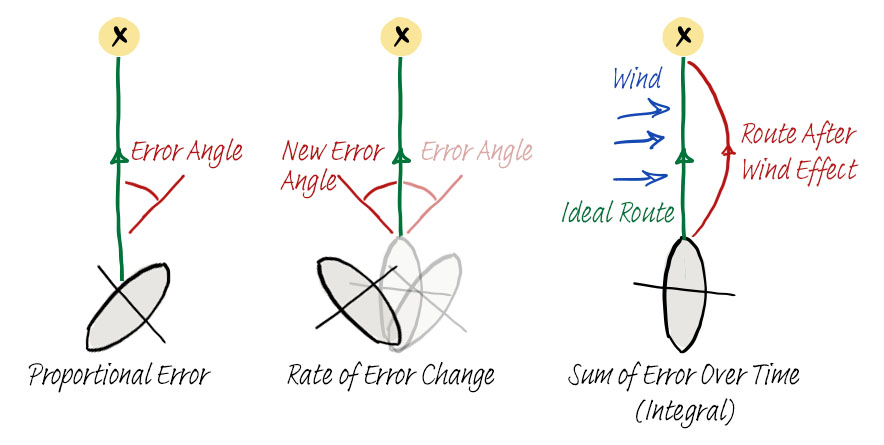
Any real-world system has some error to account and correct for and these errors can be classified mathematically in different ways. In 1911 Elmer Sperry designed a system that used calculus to better control ship steering, it had:
- Proportional error – How far off is my current direction with the direction I want to be in?
- Derivative error – How quickly is the rate of error changing?
- Integral error – What is the sum-total error over a given amount of time?
The proportional error is pretty self-explanatory: there is always some error from a true bearing and that must be constantly corrected for. The integral error helps when a ship experiences strong winds because even if the proportional error is zero (it won’t be), wind will still push the ship off-course. The derivative error is helpful because it would be easy to overcompensate for the first two errors and make the ship overshoot the desired bearing and now it is still off-course (but on the opposite side of the true bearing). Sperry’s original design used a gyroscope and was adopted by the US Navy and utilised in WW1.
Controlling Movement
Moving away from ships and onto biological nervous systems. The nerves for directly controlling movement reside in the spinal cord, however when you decide to catch a ball there is some process that happens in the brain that must decide the action to take place and pass this information to the spinal cord: the spinal cord itself is unable to make such conscious decisions. One particular pathway (known as the hyperdirect pathway) has been identified as being important when different species, including humans, encounter a physical go/stop situation: think of running for a base in rounders or baseball.
Researchers from MIT reported some interesting findings in Cell Reports, July 2022 [1]. The researchers set up an experiment whereby mice navigated a virtual reality corridor via a self-powered treadmill and upon stopping at a precise landmark location for a set amount of time they received a reward. The landmark distance was randomised to prevent learning via timing, and instead the mouse must rely on what it sees visually.
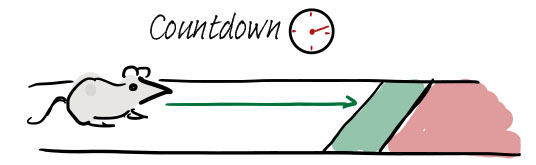
The researchers determined that mouse brains required some error correction to successfully stop at the landmark, in time, and collect their reward. This presented a dilemma:
- If the mouse does not factor in how far away it is from the landmark, it will not increase its speed to get there quick enough: it needs to keep providing a stimulus for its legs to keep running.
- If the mouse is running at full tilt it must compensate to time its braking before it overshoots the landmark and misses its reward. It must inhibit leg movement to stop.
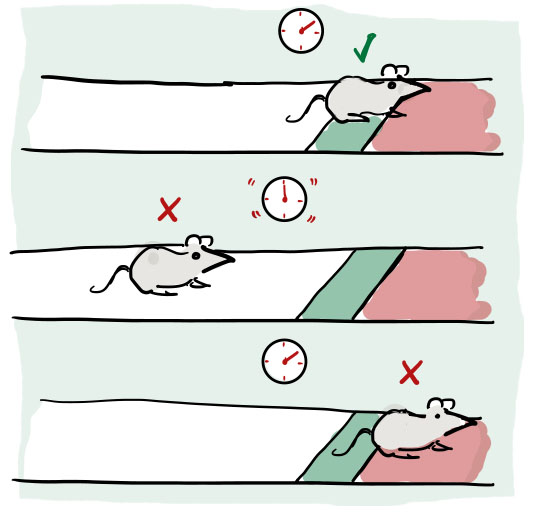
What they discovered was that the mouse’s brain compares its internal movement plan with the current moving state. And when these two states become significantly different, an “error” signal is produced that is interpreted as a stop signal. Again, the same dilemma is presented:
- If the mouse just reacts to receiving a single error signal, it will begin stopping too soon and fall short of the landmark.
- The mouse needs to sum-total the error signal over time – otherwise known as integration in mathematics – to ensure that it really is time to begin stopping. However, the visual system of the mouse is too slow to integrate the error signal quickly enough and reliably stop before at the landmark: it would overshoot and miss its reward.
What the researchers discovered is that the mouse compares the difference between the stimulatory (aka run/go) and the inhibitory (aka error/stop) signals at any given point in time, this is analogous to taking a derivative in mathematics. This allows the mouse stop soon enough to hit the landmark without overshooting. The mouse brain is using calculus, both derivatives and integrals to create an optimal movement: a movement that could not be as well executed without doing so.
The PID (Proportional, Integral, Derivative) controller
Back to ships, in 1922 a Russian-American engineer Nicolas Minorsky generalised the mathematics behind Sperry’s navigation system and what emerged was the modern PID controller – an indispensable device in modern control systems, typically implemented on a small microchip.
Modern electronic PID controllers are found in devices that require some feedback to know if they are doing the right thing. For example, temperature control of an oven, cruise control of a car, reagent mixing in a chemical plant, climate control in a building… etc.
There is an irony in how Minorsky came to develop this area of control theory, he noticed that the helmsman of naval ships provided corrective adjustments to the ships’ direction based upon:
- Current error – “I am 4°off-course, therefore correct by 4°”
- Previous error – “How far was I off-course over the last 10 seconds?”
- Rate of error – “How quickly am I approaching the direction I want?”
It appears, without much conscious thought, the helmsman was using calculus to optimally navigate the ship all along, just like our mouse trying to get its reward.
Engineering seeks to reduce complex systems into constituent parts to make them manageably understandable and gain deeper insight into the system as a whole, but human brains are the most complex systems we have encountered in the universe and if we could reduce it all to basic calculus, they would not still present so much mystery today. For all that engineering has solved it still doesn’t explain the conscious experience, but it is interesting to know that biology has also alleviated itself of some of the mundane tasks in life, in the same way that humans have done so with machines (PID controllers included).
To discuss this or Plextek's technology services, please get in touch for an initial chat: hello@plextek.com
[1] Dynamic control of visually guided locomotion through corticosubthalamic projections: Cell Reports
And thanks to The Brain Uses Calculus to Control Fast Movements | Quanta Magazine for highlighting this research.





